Our laboratory of dynamic spaces is enriched with a third experiment. We decided to test a type of movement that goes from top to bottom (and, potentially, vice-versa). We have therefore combined our Piattaforma Zero with a dynamic volume consisting of a set of panels that simulate the movement of a Yoshimura origami. The article explores in-depth how we have discretized the continuous surface of origami for construction needs. We then focus on the limits that these structures have in being translated into digital models. This is followed by the explanatory tutorial with the use of Grasshopper and specific plugins.
It is interesting to note how this example in VR, compared to the previous ones, leads to a different perception of interior/exterior for the user. Emphasizing here – depending on the degree of extension of the origami – more the aspect of privacy/exposure.

The challenge faced in this experiment is therefore to make an origami bellow structured with an oblique Yoshimura model work properly within the VR environment. Addressing the theme of origami is an interesting challenge to achieve new ways of expression for folding architecture, especially because we may have to use materials other than paper!
Usually, the folding operation of a real origami is not simply a rotation of faces around their common edges: it represents a system of interconnected movements that configures origami as a unique organism. When an origami is subjected to an external force that tries to make it closed, the folding process generates tension and deformation in the paper that can adapt to tension without tearing due to its mechanical characteristics.

This process is quite complicated to replicate using Grasshopper, especially without the usage of physics engines such as Kangaroo or FlexHopper. The main problem we faced was the incompatibility of these kind of simulators with the Rhino Compute technology, and it has therefore been necessary to solve this issue in an alternative way. The applied strategy consists of the attempt to simulate the behavior of a semi-elastic origami structure capable of withstanding a small, but adequate, deformation. When this geometry is compressed or decompressed, a small deformation, limited in a certain range of tolerance, allows for the reciprocal movement of the triangular faces of the origami without ripping. As is true for the two other geometries of the Piattaforma Zero, the folds, and so the movements, are managed with an interactive handle, inserted in the Unity scene, which modifies the folding factor from 0 to 1. When the factor is set to 0, the origami becomes flat; when the factor is set to 1, the origami reaches its maximum extension. This experiment requires some extra plugins for Grasshopper.

Let’s build it!
The geometry of the origami is developed within Grasshopper as follows:
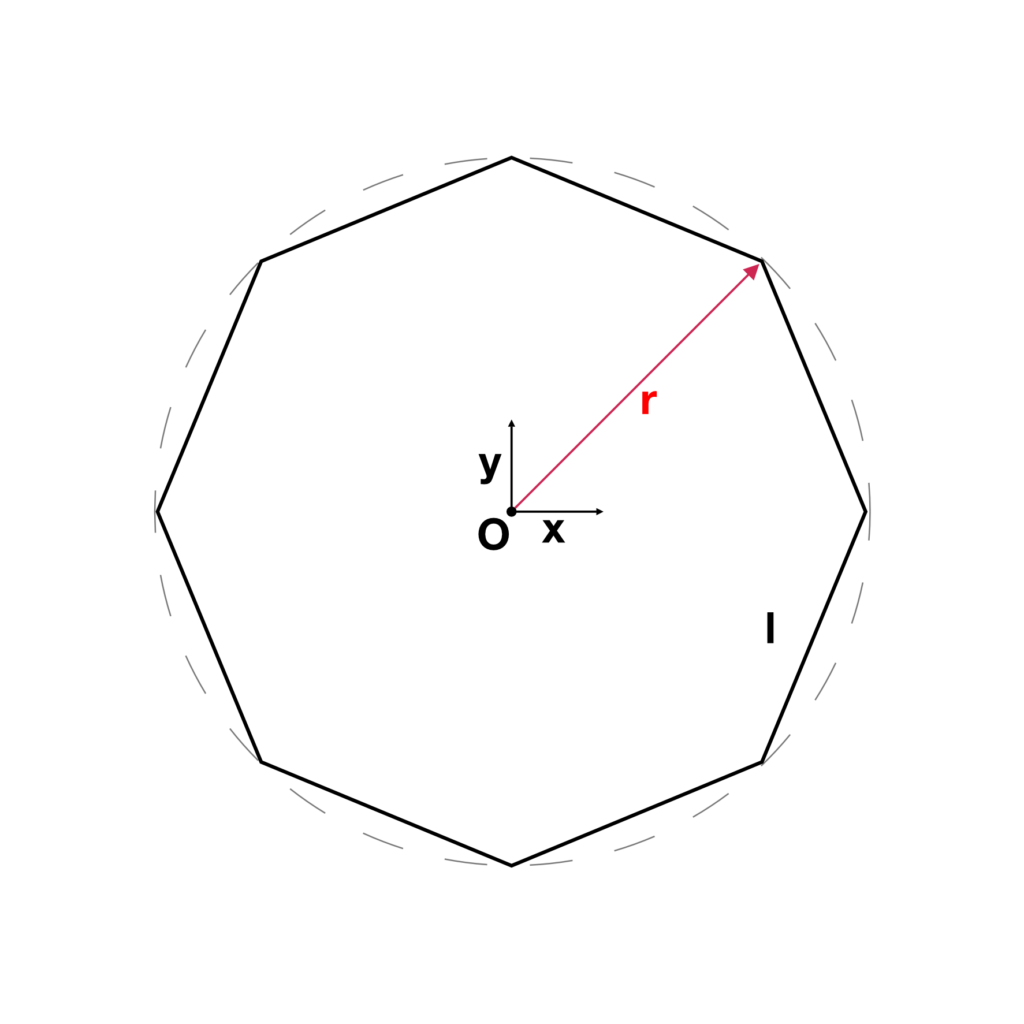
- Construction of the base polygon with a variable number of segments (n) and inscribed in a circle having a variable radius called r. Depending on the combination of r and n, each segment of the polygon has a certain length l (Fig.1).
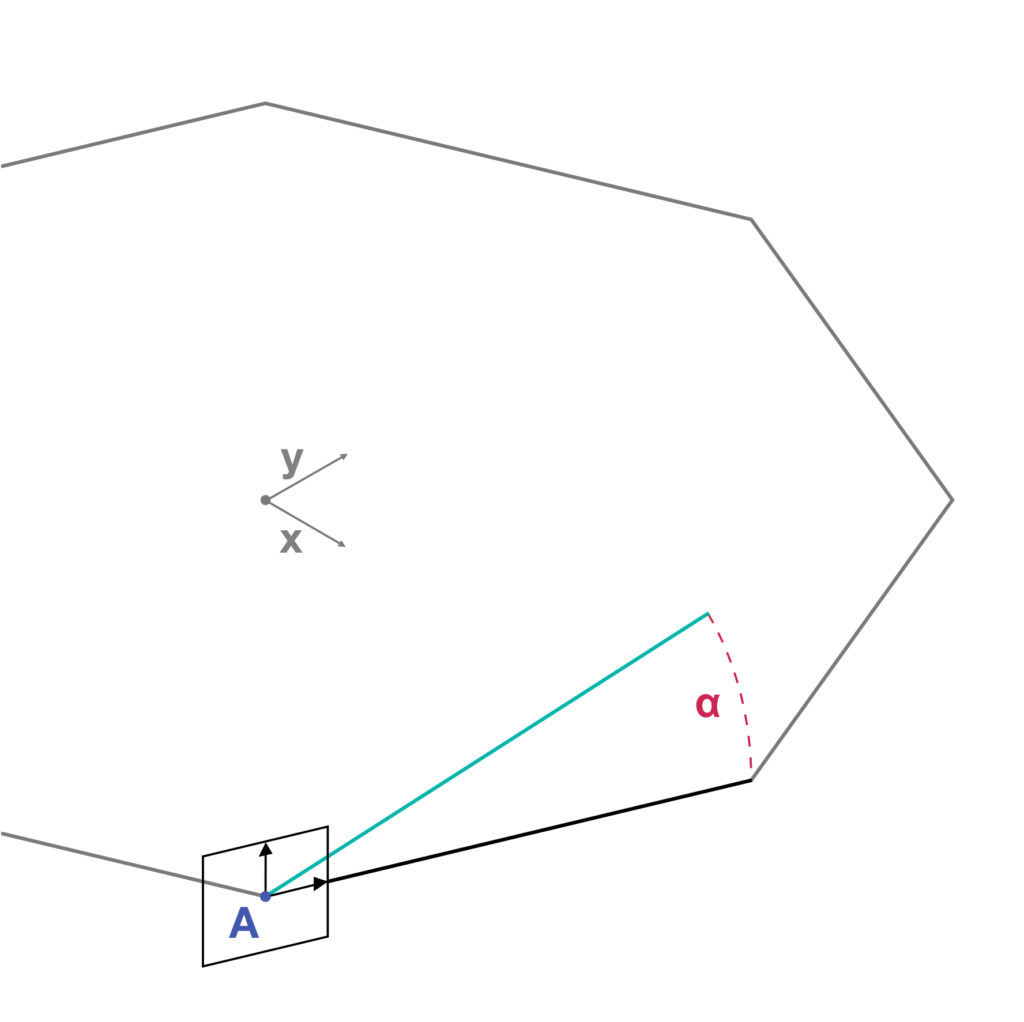
- Rotation of each segment of the base polygon by a rotation angle α and using their start points as pivots. The rotations take place along the vertical planes passing through each segment. The variable α controls the maximum extension of the modular faces of the origami. In Fig. 2 the process is applied to one segment of the base polygon which rotates from the vertex A.
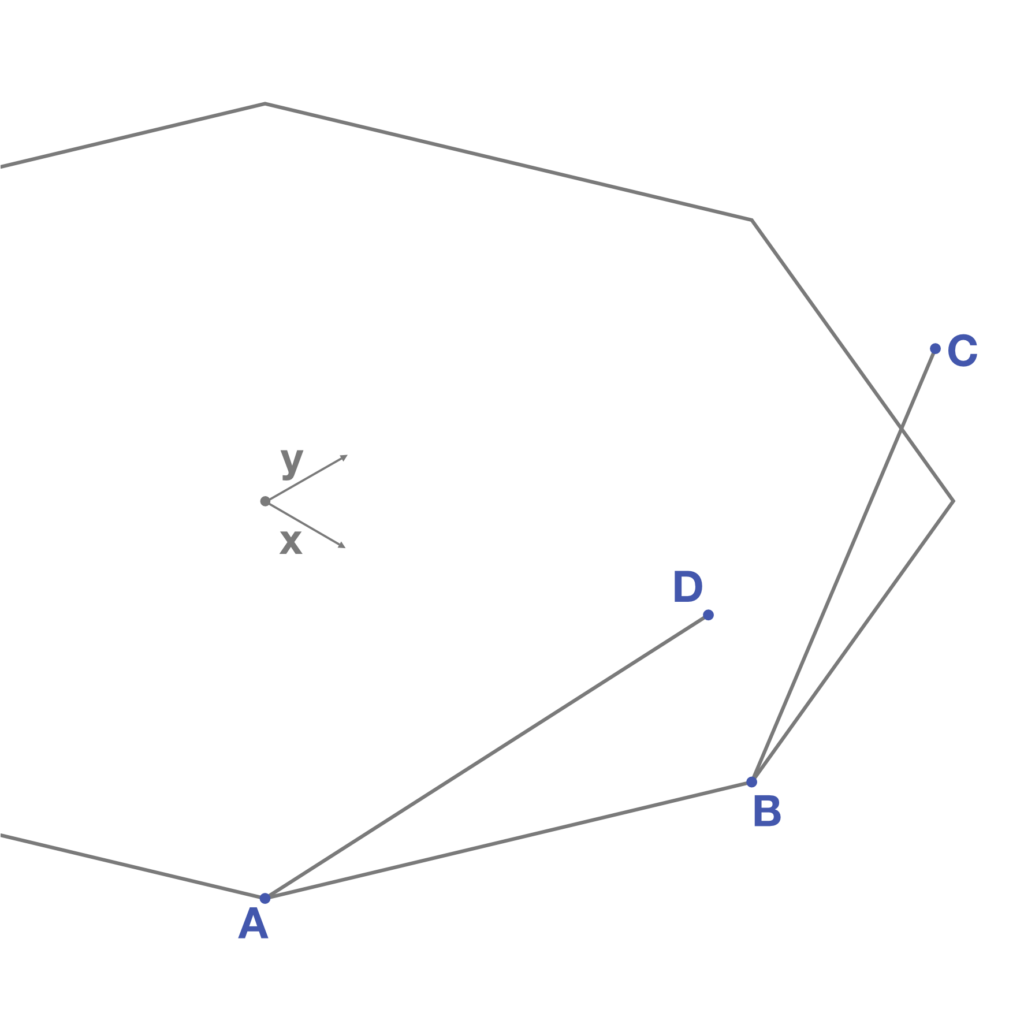
- Detection of the terminal points of each rotated segment. In Fig. 3 the process is applied to a couple of segments, detecting the points A, B, C, D.
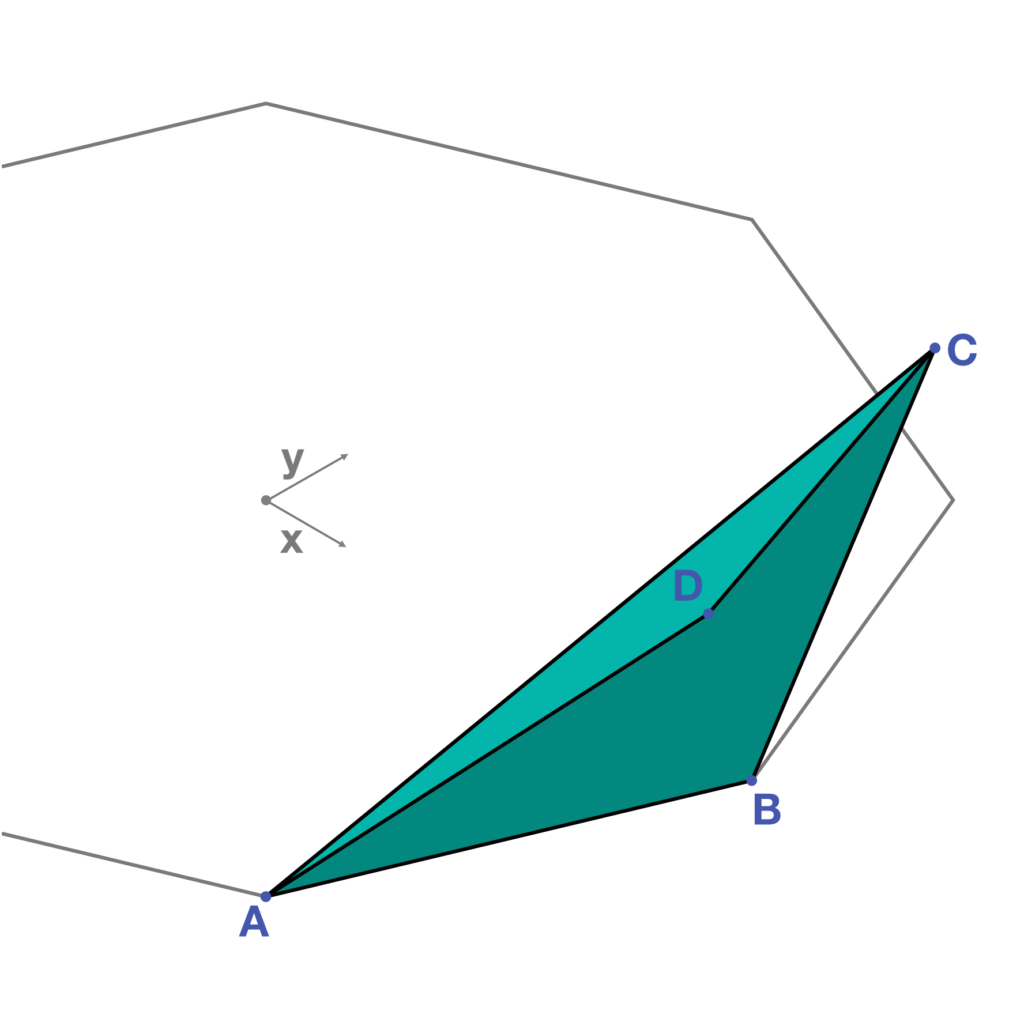
- Generation of two triangular meshes among the points A, B, C and A, C, D using the plugin WombatGH. The generated meshes represent the faces of the first module (Fig.4).
- Repetition of the process on the other segments until the first layer is closed (Fig.5).
- Looping of the process using the progressive top polygons as inputs of the algorithm until the desirable height is reached. It means that on the top polygon of each progressive layer the generation of the triangular faces is replicated (Fig.6).
- Completion of the remaining layers (Fig.7).
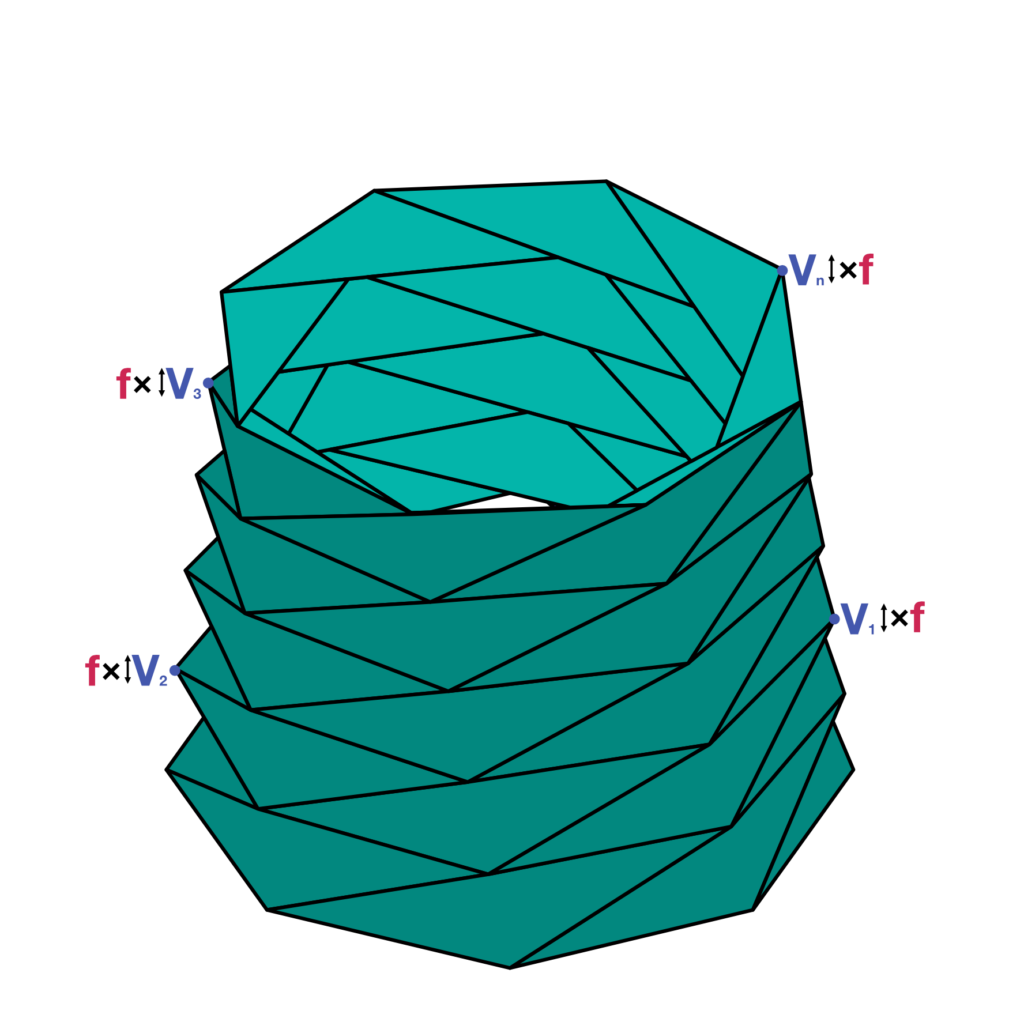
- The most crucial step is the simulation of the folding process through the translation of the n-vertices V1, V2, V3 […] Vn by n vertical vectors going from the vertices to the XY plane. Each vector has a specific length which is multiplied by a unique folding factor f set from 0 to 1. The meaning of the variable f consists of a force that tries to flatten the origami. This variable is the only one changeable dynamic parameter inside the VR experience, while all the other variables are set in Grasshopper and fixed in Unity (Fig.8).
- When the folding factor f is equal to 0, the geometry is completely flat. When it is equal to 1, the geometry is completely deployed (Fig.9).
- Cleaning process of the meshes using the Combine&Clean component of the plugin Kangaroo Physics, which removes unused and duplicate vertices of the meshes.
- Unification process of the normal vectors of the faces of the origami, in order to get an internal consistency of the meshes.
- Application of a thickness value t to the meshes on both their sides through the Offset Mesh component of the plugin Pufferfish. As a matter of visualization, the meshes are unwelded in order to mark their boundaries (Fig.10).
The origami is done. Now take your time to play with it so you can make yourself comfortable with this kind of modeling and interactive approach. You can download the commented .gh file from the link below.
With this article, our journey through the algorithmic modeling of the three geometries of the Piattaforma Zero ends. We also encourage you to experiment with the modeling of your own Grasshopper geometries and to stay tuned to our research project.
Generative Flowchart
Below you can see the recap flowchart pertaining to the generation of the geometry. This can be a useful tool to make the script of the Grasshopper definition easier and to understand the logic behind the generative procedure of this geometric example.
Pio Lorenzo Cocco, November 20, 2020